Flajolet, Hyperloglog and counting Big Data
Given a stream or tuple of items, how would you obtain the number of different items N contained in it? If you cannot memorize the items, you might want to write them on paper or at least the different ones. But what do you do when you don’t have enough paper? In this scenario, you are left with two choices. Either you can buy more paper, or you can employ probabilistic algorithms which are designed to write less, i.e., consume less paper. In this article, we briefly present the HyperLogLog (HLL) algorithm and its history.
Motivation
The problem we are concerned about here is approximate counting or cardinality estimation. It arises in many areas, such as network monitoring, search engines, or data mining. Cardinality-based methods are used to detect distributed denial of service (DDoS) attacks by counting source/target IP address pairs. Another example are databases which internally use the cardinality of columns to decide how to serve the user’s queries using the least amount of resources.
An exact count requires persisting all items on a device, e.g. using a hash table. However, storage technologies come with an inevitable tradeoff between capacity and ease of access, as measured by energy, latency, or bandwidth. That is, the expensive storage (SRAM, DRAM) is cheap to access, while the cheap storage (tape, HDD) is costly. Flash drives or SSDs sit in the middle of this spectrum and exhibit similar tradeoffs between NAND- and NOR-based architectures. Over the last four decades, progress in memory access has consistently lagged behind CPU performance improvements.
Suppose the cardinality of the input stream becomes too large. In that case, the performance of the counting application will degrade below the level you are willing to accept, or else the required hardware will become expensive. That’s where probabilistic algorithms enter the scene. They only provide approximate counts, but offer a low memory footprint which is also beneficial for runtime if memory is scarce.
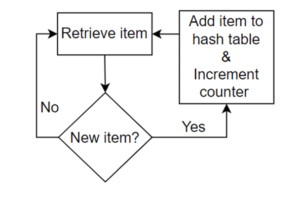
Figure 1: Flow chart for distinct count using a hash table.
Bloom filters O(n)
One approach to reduce the required memory can be to employ Bloom filters instead of hash tables [1]. A Bloom filter is a data structure that implements probabilistic set membership. The items themselves are not persisted; instead, a signature consisting of a few bits is stored in a shared bit array for each item. Hash functions are used to determine this signature, leading to a dense representation with limited capabilities. In particular, it is not possible to retrieve items, nor is it possible to delete single items, because different items may share the same bit in the array. Compared to a B-tree or hash table, the required space is drastically reduced, but still linear in N.
Bloom filters support the following Add, Check, and Delete operations:
1. Add an item to the Bloom filter.
2. Check whether an item is contained in the Bloom filter.
3. Delete all items from the Bloom filter.
You can think of a Bloom filter as a small garage where you can park an infinite number of cars. The cars are lost forever in the garage, but you can ask whether a particular car is present, to which you get an answer that may or may not be true.
Bloom filters are biased in that the response to the Check operation may return false positives, but never false negatives (perfect sensitivity). This means that the presence of items is systematically overestimated. As more items are added, the false positive rate increases, i.e. the specificity drops. In the limit of total consumption, the Bloom filter becomes a useless estimator claiming set membership for every possible item. Therefore the capacity of the Bloom filter is limited in practice by the available memory.
The length of the bit array and the number of bits per item are design parameters that determine the tradeoff between correctness (i.e. specificity or false positive rate) and capacity. Bloom filters are used by content delivery networks for efficient caching and by databases or applications in general to avoid unnecessary memory accesses or network requests. They have many applications today, but counting is not their biggest strength.
Development
Today, many database products support approximate counting aggregation functions (named approx_count_distinct or similar). That is, the queries
select count(distinct col1) from tab1 select approx_count_distinct(col1) from tab1
will usually return different results, but the second one is designed to run much faster on large tables. Many vendors have opted for the HLL algorithm when it comes to implement cardinality estimation. The name stems from required memory being of order log(log N). The required space can be sized in advance and cope with any cardinality of practical relevance.
One of the earlier papers on probabilistic counting was by Morris [2]. He presented a way to count from 1 to 130000 using a single byte of memory. The basic idea underlying HLL was developed by Philippe Flajolet and G. Nigel Martin during the early 80s of the last century. At that time, Flajolet was Director of Research at INRIA in France, while Martin was a researcher working for IBM in the UK. Both HLL and HLL++ (used by GCP BigQuery) stem from the Flajolet-Martin and PCSA algorithms (Probabilistic Counting Stochastic Average) from 1985 [3],[4]. Martin’s brilliant idea was to hash every item and extract useful information from the resulting bit pattern. Flajolet finished this idea into an algorithm ready for practical use. PCSA has log N space complexity and was used on many systems for two decades until it was gradually supplanted by HLL introduced by Flajolet and his co-workers in 2007 [5].
Both PCSA and HLL rely on stochastic averages, i.e. the input stream is divided into multiple substreams or buckets. The number of buckets m=2^p depends on the precision p and determines the overall accuracy. HLL uses a harmonic mean to combine results for each bucket to obtain the final result. Part of the hash is used to allocate items to their bucket, so that duplicate items are always sent to the same bucket. Deterministic allocation to buckets using the same hash function is essential for the algorithm. It also allows combination of algorithm states belonging to different streams to estimate cardinalities of unions. It is worth noting, that a higher number of buckets increases the cardinality threshold below which HLL performs poorly and needs to rely on other algorithms, such as Linear Counting [6].
The main reason for the performance benefit of probabilistic counting algorithms is that items are inspected once and immediately forgotten, i.e. afterwards it is impossible to tell which items were counted. This removes the need to reorganize data structures and provide space for new data. Still, it also limits the applicability to counting, e.g. removing duplicates using these algorithms is impossible.
Counting Bits
Using a hash function that assigns every bit with equal probability to zero or one, the pattern
11111111 11111111 11111111
will occur with probability 2^(-24)≈6∙10^(-8) at the end of a sequence. The occurrence or non-occurrence of these patterns can be used to estimate the cardinality of the stream. With Bash’s MD5 hash function, the bit pattern for some input can be obtained using the command:
echo <input> | md5sum | cut -c1-32 | xxd -r -p | xxd -b
The table below shows the bookkeeping used by PCSA and HLL for the first 5 items of a given bucket. For the sake of comparison, HLL is presented as counting trailing ones, instead of leading zeros [5].

Figure 2: Bookkeeping of PCSA and HLL algorithms for the first five items of a substream. In this example with 5 input values, PCSA uses the value R=3 to estimate the cardinality.
For every bucket PCSA relies on a bit array r which is initialized to 0. For given input item x the number of trailing ones in the hash result is counted, and the appropriate bit in the bit array is set using the assignment
r = r | (~x & (x+1)) ,
where |, &, ~ denote the bitwise operators for inclusive disjunction (or), conjunction (and), and complement (not). At the end of the aggregation, most left bits will be zero, while most right bits will be one. Finally, PCSA averages the number of consecutive trailing ones among the buckets’ bit arrays and returns the estimate N=2^(R_AVERAGE )/0.7735.
In contrast to PCSA, HLL simply remembers the maximum value of consecutive trailing ones previously encountered in each bucket. Whereas PCSA needs to allocate several bytes for each bucket, HLL relies on a single byte leading to lower memory usage. For the same number of buckets, PCSA offers better accuracy than HLL; however, the overall space-accuracy tradeoff is better for HLL. HLL maintains the same accuracy with less memory but more buckets than PCSA.
The memory-accuracy tradeoff for HLL and most approximate counting algorithms is quadratic, i.e. cutting the average error in half requires four times more memory. The results returned by PCSA and HLL are independent of the record order.
Applications
The databases Oracle, MS Server, Snowflake, AWS Redshift, Azure Synapse Analytics, Redis, and others rely on HLL implementations for approximate counting. An exception is Google with its GCP BigQuery service that uses HLL++, which introduces algorithmic improvements at a range of small cardinalities [7].
Snowflake, Redshift, and Bigquery claim average relative errors below two percent. Still, there are no guarantees for single runs, and it is possible (but tedious) to prepare data that fools the algorithm.
Apart from the APPROX_COUNT_DISTINCT function, these databases provide several HLL functions that allow managing the cardinality estimation using sketches. In particular, it is possible to estimate the cardinality of unions using already gathered statistics, i.e., building hierarchies and providing estimates for every layer using information gathered at the bottom. For instance, you may count unique events per 10-minute interval and store this information using the sktech data type. This information can then be reused to build unique counts per hour, day, week, etc..
Snowflake and Redshift also allow exporting the algorithm state as JSON objects. BigQuery allows the user to configure the precision to any value between 10 and 24, leading to different accuracies. In contrast, Snowflake and Redshift use fixed precisions of 12 and 15, respectively.
HLL is only one of several approximate algorithms supported by these databases. Other examples are the generation of quantiles or identification of the most frequent records using Snowflake’s APPROX_PERCENTILE and APPROX_TOP_K functions. These memory-saving aggregation functions can help to design reporting solutions over large data sets that reflect the most recent data.
Today, HLL is one of the best-known algorithms for approximate counting and has found widespread adoption in many systems since its invention 15 years ago. It allows to count datasets of any cardinality using minimal resources, is suited for adoption in stream processing, and can run in parallel. Significant improvements with respect to HLL seem unlikely, so that HLL may stay with us for some time. You may also find the presentations from Flajolet and Sedgewick interesting [8],[9]. Happy counting!
Many thanks to Prof. Conrado Martínez from the Universitat Politècnica de Catalunya for his useful remarks.
References
[1] Onur Mutlu, “Computer Architecture Lecture 2a: Memory Refresh”, 2019
[2] Robert Morris, “Counting large numbers of events in small registers”, 1978
[3] Philippe Flajolet, G. Nigel Martin, “Probabilistic Counting Algorithms for Data Base Applications”, 1985
[4] Philippe Flajolet, “Approximate Counting: A Detailed Analysis”, 1985
[5] Philippe Flajolet, Éric Fusy, Olivier Gandouet, Frédéric Meunier, “HyperLogLog: the analysis of a near-optimal cardinality estimation algorithm”, 2007
[6] Kyu-Young Whang, Brad T. Vander-Zanden, Howard M. Taylor, “A Linear-Time Probabilistic Counting Algorithm for Database Applications”, 1990
[7] Stefan Heule, Marc Nunkesser, Alexander Hall, “HyperLogLog in Practice: Algorithmic Engineering of a State of The Art Cardinality Estimation Algorithm”, 2013
[8] Philippe Flajolet, “Probabilistic Counting: from analysis to algorithms to programs”, 2007
[9] Robert Sedgewick, “Cardinality Estimation”, 2018

